type
status
date
slug
summary
tags
category
icon
password
写在前面:
这门课应该是本科阶段第二喜欢的课了,其实上到这里结果如何已经不重要了。程磊老师讲的真心好,课程内容也是我特别感兴趣的一块,算是和高代II平行的一门课吧,之前学线性映射中很多不理解的东西都打通了,这门课里也有很多东西可以和高等代数结合起来,现在还记得写第一次作业的1.73时用维数定理、Kernel、Image这些高代知识解决那道明显是超纲的题的快感,好像一下子就看清了这道题的本质,也彻底打通了大一时候很难理解的不变子空间和Jordan标准型的关系(即便这道题我记得在学高代的时候应该是见过的)。很多时候听着听着自己的思维就跑到其他问题上去了,以至于程老师叫我的时候我好像都没在听课(x,可能我就是那个上课不注意听的反例吧。程老师真的是为数不多的能把东西说特别清楚的老师,还能和同学像朋友一样互动。应该是本科阶段最积极的一门课了,次次都坐第一排,希望我也能保研(bushi
开个坑在复习的时候记录一些知识点,不出意外和之前的那些notes一样是毫无营养的抄书,只有抄的过程才是有意义的,写的东西毫无营养(
1 矩阵代数基础
线性方程组解的个数
- 唯一解:
- 无穷多解:
- 无解:
向量的内积与范数
典范内积:
加权内积:
其中是正定Hermitian矩阵。
常用的向量范数:
(1)范数(0范数)
(2)范数(和范数、1范数)
(3)范数(Eculidean范数、Frobenius范数)
(4)范数(无穷范数、极大范数)
(5)范数(Holoder范数)
函数向量的内积与范数:
随机向量的内积与范数:
向量的外积:
矩阵的内积与范数
矩阵的向量化:
内积的推广:
诱导范数:
诱导-范数:
当取不同的值时,有如下范数的定义:
(1)绝对列和范数
(2)矩阵的最大奇异值
(3)绝对行和范数
“元素形式”范数:
(1)范数:
(2)Frobenius范数:
(3)范数:
随机向量
联合累计分布函数(CDF):
概率密度函数(PDF):
均值向量:
相关矩阵:
为Hermitian矩阵。
自协方差矩阵:
自相关矩阵和自协方差矩阵的关系:
互相关矩阵:
互协方差矩阵:
互相关矩阵和互协方差矩阵的关系:
实高斯白噪声向量:
对于一个实高斯白噪声向量,其PDF为
复高斯白噪声向量:
对于一个复高斯白噪声向量,其PDF为
Moore-Penrose逆矩阵
令是任意矩阵,称矩阵为的广义逆矩阵,若满足
(1)
(2)
(3)
(4)
矩阵的直和和Hadamard积
直和:
Hadamard积:
Kronecker积:(默认为右)
向量化与矩阵化
按列堆栈:
按行堆栈:
2 特殊矩阵
置换矩阵
一个正方矩阵是置换矩阵,若它的每一行和每一列有且仅有一个非零元素1,容易验证是正交矩阵。
互换矩阵
交换矩阵
一个的矩阵为交换矩阵,若它对矩阵满足
广义置换矩阵
相似矩阵和相似变换
存在一个非奇异矩阵使得,称。
相似变换:
相似矩阵的特征值相同,特征向量存在线性变换关系。
Hadamard矩阵
称为Hadamard矩阵,若它的所有元素取或,且
第一列和第一行所有元素为的Hadamard矩阵称为规范化Hadamard矩阵。
只有当或者是的整数倍时,Hadamard矩阵才存在。
容易验证是标准正交矩阵,且
令则规范化的标准正交Hadamard矩阵具有通用构造公式:
其中
3 矩阵微分
Jacobian矩阵与梯度矩阵
行偏导:
Jacobian矩阵:
对于实标量函数
对于实矩阵函数
列偏导:
梯度矩阵:
对于实标量函数
对于实矩阵函数
一阶实矩阵微分
矩阵微分:
的微分:
矩阵乘积的微分:
标量函数的Jacobian矩阵辨识:
对于实标量函数
Hessian矩阵
共轭梯度与复Hessian矩阵
复变元向量的微分:
复变元向量的全Hessian矩阵:
4 梯度分析与最优化
实变量函数无约束优化的梯度分析
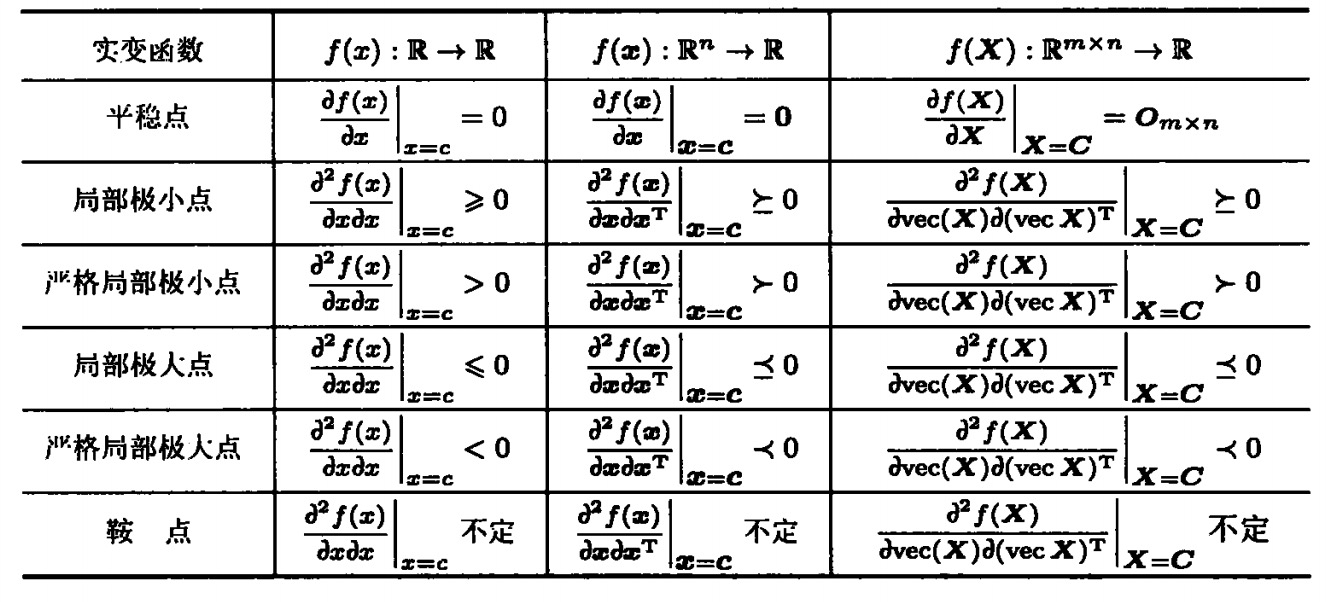
复变函数的平稳点和极值点条件

无约束最小化问题的梯度分析——闭式解
令实变函数的梯度或复变函数的共轭梯度为0.
平滑凸优化的一阶算法——梯度下降方法
线搜索法:
精确线搜索法(全松弛准则):
Goldstein-Armijo准则:
记
求,使得
即用两条线限制每一步的搜索范围。
平滑凸优化的二阶算法——牛顿法
修正牛顿法:
拟牛顿法:
约束优化算法——Lagrange乘子法
考虑优化问题
则可以构造Lagrangian函数:
其中有约束条件.
对于等式约束问题,令各个变量的梯度为0即可求得。
约束优化算法——罚函数法
同样考虑上述的优化问题,其基本原理是,将约束优化问题通过罚函数转化成反应优化问题和约束条件的无约束极小化问题。
记为的可行集,那么有如下两种方式进行转化:
加性罚函数:
其中罚函数.
乘性罚函数:
其中罚函数.
通常采用加性罚函数。
对于等式约束,考虑罚函数
对于不等约束,考虑外罚和内罚两种情况:
外罚函数(对所有都进行惩罚):
内罚函数(阻止离开):
混合罚函数即对外罚函数和内罚函数进行加权。
5 矩阵方程求解
最小二乘法
求解矩阵方程,考虑无解的情况,想要找到近似解,使得
令代价函数为
则有
- 且时:
一定有是非奇异矩阵,即,因此
- 且时:
- 时
方程欠定,不可辨识。
Gauss-Markov定理
方程的最小二乘解是方程的最优无偏估计。
同时也是最大似然估计。
数据最小二乘法
解矩阵方程,其中数据矩阵在观测时存在误差,即观测到的满足
目标是找到一个解,使得
构造Lagrange函数:
令,有
令,有
代入得
即
因此
带回原目标函数,有
因此数据最小二乘问题等价为优化问题
Tikhonov正则化
考虑当代价函数加入一个正则项时,有
令
使,有
即,因此
总体最小二乘法
解矩阵方程,其中和的观测均存在误差,即观测到的满足
因此问题变成
约束条件可以写成
即
令
此时问题变成
此时问题转化为一个特殊的数据最小二乘问题,因此可进一步等价为优化问题
上式的形式称为Rayleigh商。
6 特征分析
特征分解(EVD, Eigen Value Decomposition)
矩阵具有个特征值,其对应的个单位特征向量为,记
则可分解为
特征多项式与Caley-Hamiton定理
特征多项式:
称
为矩阵的特征多项式
Caley-Hamiton定理:
标准正交变换
给定一组相关的随机变量,希望通过某个线性变换,把它变成另外一组统计不相关的随机变量。
令为一随机向量,其均值向量为,协方差矩阵为,其EVD为希望能够找到一个线性变换,使得当时,有
前者是显然的,后者有
即,由于为正交矩阵,因此.
迷向圆变换
进一步地,找到一个线性变换,使得当时,有
因此有.
离散Karhonen-Loeve变换(重构最优性)
令是一个零均值的随机向量,其自相关矩阵为.希望找到一个线性正交变换
其中是一酉矩阵。于是可以表示成的列向量的线性组合
为了减小变换后的系数的个数,假设只使用前个系数来表示,有
误差为
由此可以得到均方误差
因此可构造约束优化问题
构造Lagrange函数
令其共轭梯度为0有
因此在均方误差最小时,有
即若有个大特征值,个可以忽略的特征值,可以通过上式近似代替.
Rayleigh商
设为Hermitian矩阵,称下式为其Rayleigh商
其最大值,最小值.
广义Rayleigh商
令,得
7 奇异值分析
数值稳定性与条件数
当线性方程组存在扰动时,即
则有
称为条件数,反应解的扰动情况。条件数很大时称矩阵为病态的。
奇异值分解(SVD, Singular Value Decomposition)
令,则存在酉矩阵,使得
其中,。
且,按从大到小的顺序排列,称为的奇异值。因此有
并且为矩阵和的第个特征值,为的特征向量组成的矩阵,为的特征向量组成的矩阵。
矩阵范数与奇异值的关系
- 作者:Tannin Rachel
- 链接:https://www.tanninrachel.ren/article/matrix
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。



